Введение
Научно-исследовательские изыскания в области порядкового счета бинарно-мануальным способом (иначе говоря, с помощью загибания пальцев) позволяют утверждать, что повсеместно используемая методика является далеко не единственной. Более того, она не только не оптимальна, но и поразительно несовершенна. Подавляющее большинство людей считают, что загибая пальцы на обеих руках, возможно досчитать лишь до десяти. Очевидно, что с математической точки зрения это в корне неверно. [1] В самом деле, положив в основу тот факт, что каждый палец имеет как минимум два возможных состояния (разогнут/загнут), мы получаем в распоряжение десять бит информации. Следовательно, протяженность интервала, в котором возможно осуществление порядкового счета, составляет 210 = 1024 единицы.
Целью настоящей работы является разработка схемы мануального счета, позволяющего с наилучшей результативностью использовать возможности подручных пальцев. Актуальность работы обусловлена тем, что повсеместно применяемая методика порядкового счета на пальцах была разработана около 200 тысяч лет назад и на сегодняшний день морально устарела.
1. Общая информация о двоичной системе счисления
Двоичная система счисления — это положительная целочисленная система счисления, позволяющая представить различные численные значения с помощью двух символов, условно обозначаемых «0» и «1». [2]
В рамках настоящей работы представляет интерес схема перевода чисел из десятичной системы в двоичную и обратно. Для преобразования числа из двоичной в десятичную систему используется метод Горнера, состоящий в суммировании цифр слева направо, умножая ранее полученный результат на основу системы (в рассматриваемом случае — число 2). Например, двоичное число 1011011 переводится в десятичную систему следующим образом:
0 × 2 + 1 = 1 1 × 2 + 0 = 2 2 × 2 + 1 = 5 5 × 2 + 1 = 11 11 × 2 + 0 = 22 22 × 2 + 1 = 45 45 × 2 + 1 = 91 Результат: 10110112 = 9110
Таким образом, в десятичной системе это число будет записано как 91.
Для преобразования числа из десятичной системы счисления в двоичную существует следующая схема. Число делится на 2 и в остаток от деления записывается 1 или 0. Затем результат деления опять делится на 2 и снова записывается остаток. Деление продолжается до тех пор, пока в делимом не окажется 1. Далее необходимо записать последовательно числа из остатка, начиная с конца: полученное число и будет искомым.
Например, необходимо перевести в двоичную систему число 19.
19 / 2 = 9 с остатком 1 9 / 2 = 4 c остатком 1 4 / 2 = 2 с остатком 0 2 / 2 = 1 с остатком 0 1 / 2 = 0 с остатком 1 Результат: 1910 = 100112
2. Сущность предлагаемой схемы порядкового счета
Предлагаемая схема основывается на том, что двоичная система счисления является позиционной, то есть один и тот же числовой знак имеет различные значения в зависимости от того места (разряда), где он расположен. [3] Суть рассматриваемой схемы мануального счета состоит в том, что каждому пальцу ставится в соответствие определенный разряд двоичного числа. Нулевой разряд поставлен в соответствие большому пальцу правой руки, обращенной ладонью к субъекту счета; первый разряд соответствует указательному пальцу, второй – среднему и т.д.
Предлагается к использованию термин дактилобит – отображение значения бита с помощью пальца. Загнутый палец соответствует единице в соответствующем разряде двоичного числа, распрямленный – нулю.
Выбор большого пальца в качестве нулевого разряда обусловлен тем, что при порядковом счете именно нулевой разряд наиболее часто меняет свое значение; и именно большой палец на основе серии опытов признан автором наиболее подходящим для постоянного сгибания-разгибания.
В случае превышения четвертого разряда (превышения числа 31 в десятичной системе) необходимо ввести в рассмотрение левую руку, также повернутую ладонью к производящему счет. Таким образом, пятому разряду ставится в соответствие мизинец левой руки, шестому – безымянный палец и т.д. На рисунке 1 представлена схема дактилобито-разрядного соответствия. Для каждого дактилобита указан соответствующий разряд.
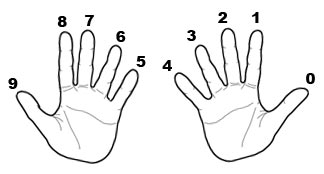
Собственно счет производится последовательным загибанием дактилобитов в соответствии с надлежащим двоичным числом. В таблице 1 приведены 32 возможные схемы расположения пальцев правой руки при порядковом бинарном счете от 00000 до 11111.
Таблица 1. Схема расположения пальцев правой руки при порядковом бинарно-мануальном счете в интервале [0; 31]
|
|
Аналогичным образом с помощью левой руки формируются дальнейшие составляющие числового ряда. Следует обратить внимание, что порядок загибания пальцев на левой руке отличен от порядка, приведенного в таблице 1. Это обусловлено анатомией левой кисти, зеркальной по отношению к правой. Однако же общий принцип, очевидно, остается неизменным. На рисунке 2 в качестве примера изображено отображение дактилобитами числа 620.

Не рекомендуется на длительное время задерживать дактилобитовое отображение числа 27 в людных местах по этическим причинам.
3. Оптимизация системы
К недостаткам описанной методики счета можно отнести следующее:
1) Кажущаяся сложность освоения метода;
2) Ограниченный числовой диапазон счета.
Таким образом, оптимизацией системы будет являться преодоление выделенных недостатков.
Что касается первого пункта, то есть якобы высокой сложности овладения методом, то он несостоятелен. Метод бинарного счета намного проще метода слепой десятипальцевой печати на клавиатуре, при котором каждый палец «запоминает» от четырех до шестнадцати и более рабочих позиций. [4] Однако же навык бинарного счета совершенно неизвестен, в отличие от метода слепой печати, при несопоставимой важности этих навыков: очевидно, считать каждому человеку приходится чаще, чем набирать текст. Эмпирически легко убедиться в том, что понимание принципа дактилобитового счета при незначительной тренировке усваивается на подсознательном уровне.
Преодоление второго недостатка сводится, очевидно, к расширению диапазона счета. В двоичной системе счисления добавление одного дополнительного бита увеличивает числовой диапазон вдвое. Следовательно, добавив к десяти дактилобитам лишь один бит, становится возможным производить счет до 2047, добавив два бита – до 4095 и т.д.
Таким образом, в качестве базовой оптимизации предлагается расширение диапазона используемых битов за счет подручных средств. Строго говоря, в роли подобных дополнительных битов может выступать произвольная сущность, отвечающая двум условиям:
- наличие двух четко выраженных состояний сущности (условных 0 и 1);
- легкость перевода сущности из одного состояния в другое, причем осуществляемого только по воле субъекта.
В качестве двух дополнительных битов возможно использовать верхний свободных край век. Иначе говоря, зажмуренный первый (правый) глаз соответствует состоянию 01, левый – 10, оба – состоянию 11. Отсутствие визуального контроля, неизбежное в таком случае, как было сказано выше, не должно явиться препятствием к продолжению счета.
Однако же практика показывает, что в повседневном обиходе случаи, когда возникает необходимость на пальцах досчитать до 2047, исключительно редки. Таким образом, более целесообразным представляется использование дополнительных битов для преодоления проблемы невозможности оперирования ненатуральными (т.е. дробными и отрицательными) числами. К примеру, единица в одном из глазных битов может отвечать за знак «минус» перед числом, таким образом, расширяя числовой ряд в сторону отрицательных значений. . На рисунке 3 в качестве примера представлено отображение числа «-25».
Если же требуется использование дробной части, решением проблемы является помощь второго дактилоносителя, ответственного за дробь. Использование пальцев ног в данном случае не представляется целесообразным.
Заключение
Используйте разработанную инновационную систему мануального счета на основе нанотехнологий, и будет вам щастье!
Литература
1. http://bash.org.ru/quote/399340
2. http://ru.wikipedia.org/wiki/Двоичная_система_счисления
3. http://ru.wikipedia.org/wiki/Позиционная_система_счисления
4. http://upload.wikimedia.org/wikipedia/ru/thumb/9/92/Solo_on_the_keyboard.png/300px-Solo_on_the_keyboard.png































